PolyhedronNet
PolyhedronNet: The Ultimate Framework for 3D Polyhedron Representation Learning
Transforming polyhedra into powerful vector representations for 3D shape analysis
Dazhou Yu, Genpei Zhang, Liang Zhao
Department of Computer Science, Emory University
Published as a conference paper at ICLR 2025
What is PolyhedronNet?
PolyhedronNet is a groundbreaking framework designed specifically for learning representations of 3D polyhedron objects. As the first dedicated solution for polyhedron representation learning, PolyhedronNet addresses the unique challenges of working with these complex geometric structures.
A polyhedron (plural: polyhedra) is a 3D geometric shape with flat polygonal faces, straight edges, and sharp vertices. Common examples include cubes, pyramids, and more complex shapes like dodecahedrons. Polyhedra are fundamental building blocks in 3D modeling, computer graphics, architecture, and many scientific disciplines.
Our innovative approach transforms polyhedra into comprehensive vector representations that capture both structural and geometric properties, enabling advanced analysis, classification, and retrieval of 3D shapes with unprecedented accuracy.
Why Polyhedron Representation Matters
- Enables efficient 3D shape analysis and comparison
- Powers applications in computer graphics and CAD
- Facilitates architectural and engineering design
- Supports 3D printing and manufacturing
PolyhedronNet Advantages
- Surface-attributed graph representation captures complete polyhedron structure
- Rotation and translation invariant for consistent analysis
- State-of-the-art performance on polyhedron classification and retrieval
- Open-source implementation for research and applications
Abstract
Ubiquitous geometric objects can be precisely and efficiently represented as polyhedra. The transformation of a polyhedron into a vector, known as polyhedra representation learning, is crucial for manipulating these shapes with mathematical and statistical tools for tasks like classification, clustering, and generation.
This study proposes PolyhedronNet, a general framework tailored for learning representations of 3D polyhedral objects. We introduce the concept of the surface-attributed graph to model vertices, edges, faces, and their geometric interrelationships within a polyhedron, achieving rotation and translation invariance while preserving discriminative power.
Our experimental evaluations on four distinct datasets (MNIST-C, Building, ShapeNet-P, and ModelNet-P), encompassing both 3D polyhedral object classification and 3D shape retrieval tasks, substantiate PolyhedronNet's efficacy in capturing comprehensive and informative representations of 3D polyhedral objects. Code and data are available at github.com/dyu62/3D_polyhedron.
PolyhedronNet Methodology
Our innovative approach to polyhedron representation learning
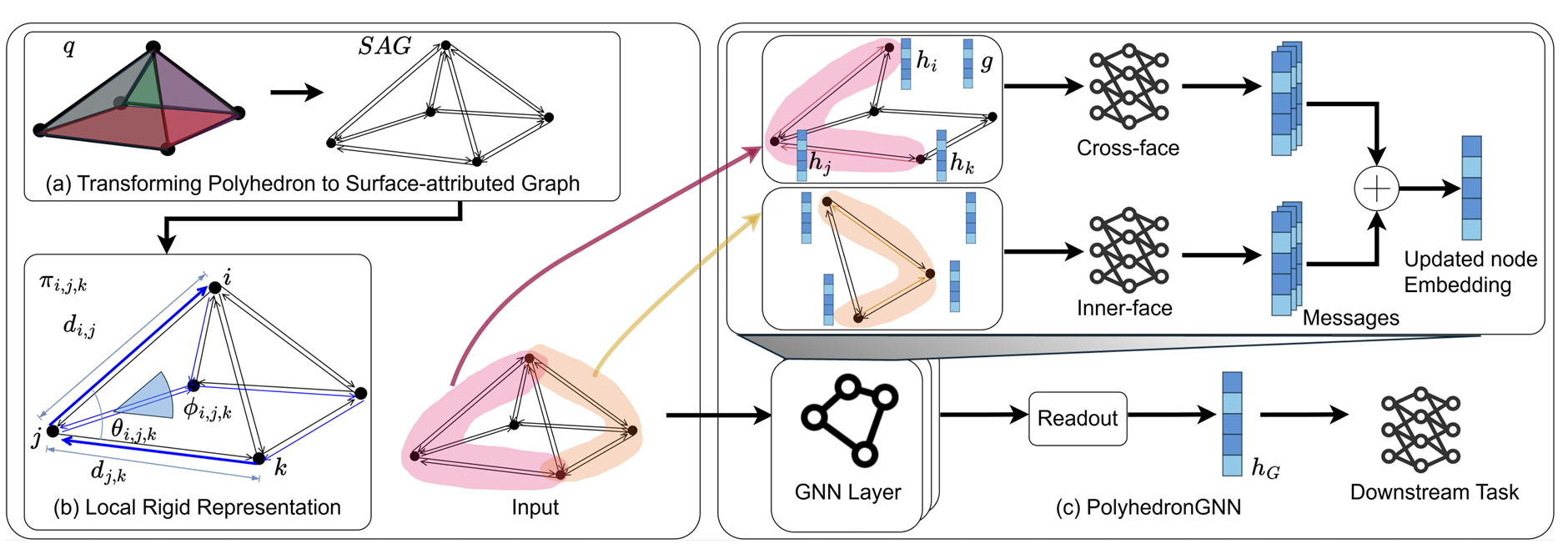
Figure: The PolyhedronNet framework for polyhedron representation learning consists of three main components:
- Transforming a polyhedron into a Surface-attributed Graph (SAG)
- Computing Local Rigid Representation with geometric relationships
- PolyhedronGNN for learning representations through message passing
Surface-Attributed Graph
A novel graph representation that captures vertices, edges, faces, and their relationships in a polyhedron through face-hyperedges, enabling comprehensive polyhedral graph transformation.
Local Rigid Representation
A five-tuple geometric representation that preserves structural information while achieving rotation and translation invariance in 3D polyhedra, crucial for consistent polyhedron representation learning.
PolyhedronGNN
A specialized graph neural network for 3D polyhedra that aggregates local representations through intra-face and inter-face message passing, enabling effective polyhedron representation learning.
Technical Innovation in Polyhedron Representation
PolyhedronNet introduces several key innovations in the field of polyhedron representation learning:
- Face-centric representation: Unlike previous methods that focus only on vertices or edges, PolyhedronNet explicitly models faces as first-class entities in the polyhedron representation.
- Heterogeneous message passing: Our approach enables information flow between different structural elements of a polyhedron (vertices, edges, and faces).
- Invariant geometric features: PolyhedronNet computes local geometric features that are invariant to rotation and translation, ensuring consistent polyhedron representation regardless of orientation.
Polyhedron Analysis Results
Benchmark performance on polyhedron classification and retrieval tasks
Polyhedra Datasets
MNIST-C Polyhedra
13,742 samples3D digit polyhedra with color-coded faces for rotation invariance testing in polyhedron classification
Building Polyhedra
5,000 samples3D building polyhedra from OpenStreetMap for architectural polyhedron shape analysis
ShapeNet-P Dataset
2,122 samples15 object categories from ShapeNetCore converted to polyhedra for diverse 3D object classification
ModelNet-P Dataset
1,303 samples14 object categories from ModelNet40 converted to polyhedra for 3D shape retrieval evaluation
PolyhedronNet outperforms all comparison methods in 3D polyhedron classification:
- MNIST-C: 85.8% accuracy (vs. 43.5% for next best method) in polyhedron digit classification
- Building: 98.0% accuracy with perfect AUC of 1.0 in architectural polyhedron classification
- ShapeNet-P: 62.7% accuracy with 93.6% AUC in diverse polyhedron object classification
- ModelNet-P: 43.5% accuracy with 82.4% AUC in challenging polyhedron classification
Key Research Findings in Polyhedron Analysis
- Face attributes significantly improve performance in polyhedra representation learning (up to 49.8% accuracy gain)
- Heterogeneous message passing in PolyhedronGNN is crucial for capturing complex geometric relationships in polyhedra
- Optimal performance achieved with 4 GNN layers and 256 hidden dimensions for 3D polyhedron representation learning
- PolyhedronNet effectively handles ambiguity in rotated polyhedra, demonstrating rotation and translation invariance
PolyhedronNet Code & Resources
Open-source implementation for polyhedron representation learning
GitHub Repository
Our implementation of PolyhedronNet is available on GitHub, including code, documentation, and instructions for reproducing our experiments on 3D polyhedron classification and polyhedron shape retrieval.
github.com/dyu62/3D_polyhedronPolyhedra Datasets
Access to MNIST-C, Building, ShapeNet-P, and ModelNet-P datasets for 3D polyhedra research and benchmarking.
Download Polyhedra DatasetsResearch Paper
Access our paper on PolyhedronNet published at ICLR 2025 and supplementary materials on polyhedron representation learning.
Download PolyhedronNet PaperFrequently Asked Questions
What is PolyhedronNet?
PolyhedronNet is a novel framework for learning representations of 3D polyhedral objects. It introduces the concept of surface-attributed graphs to model vertices, edges, faces, and their geometric interrelationships within a polyhedron.
How does PolyhedronNet represent polyhedra?
PolyhedronNet represents polyhedra using a three-step process: 1) Transforming a polyhedron into a Surface-attributed Graph (SAG), 2) Computing Local Rigid Representation with geometric relationships, and 3) Using PolyhedronGNN for learning representations through message passing.
What are the applications of polyhedron representation learning?
Polyhedron representation learning is crucial for manipulating 3D shapes with mathematical and statistical tools for tasks like 3D object classification, clustering, retrieval, and generation. It has applications in computer graphics, CAD, architecture, and 3D modeling.
How does PolyhedronNet perform in polyhedron classification?
PolyhedronNet outperforms all comparison methods in 3D polyhedron classification, achieving 85.8% accuracy on MNIST-C, 98.0% accuracy on Building dataset, 62.7% accuracy on ShapeNet-P, and 43.5% accuracy on ModelNet-P.
What makes polyhedron representation different from other 3D shape representations?
Polyhedron representation specifically focuses on 3D shapes with flat polygonal faces, straight edges, and sharp vertices. Unlike point clouds or voxels, polyhedra preserve exact geometric information and topological structure, making them ideal for precise 3D shape analysis and manipulation.